Providing Class 9th Maths formulas list chapter-wise that makes your work easy.
Number Systems
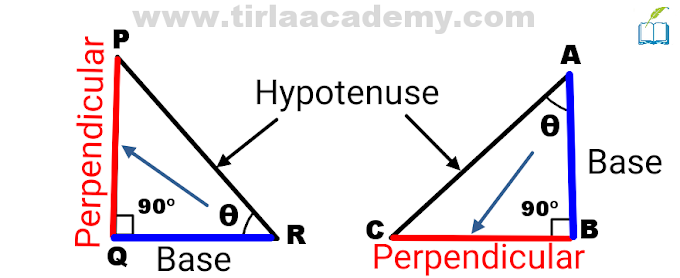
⇒ Pythagoras Theorem:- H² = P² + B²
⇒ (a+b)²=a²+2ab+b²
⇒ (a-b)²=a²-2ab+b²
⇒ (a+b)(a-b)=a²-b²
⇒ a-ᵐ = 1/aᵐ
⇒ aᵐ×aⁿ=aᵐ⁺ⁿ
⇒ aᵐ÷aⁿ=aᵐ⁻ⁿ
⇒ (aᵐ)ⁿ=aᵐⁿ
⇒ aᵐ×bᵐ=(ab)ᵐ
⇒ aᵐ÷bᵐ=(a÷b)ᵐ
⇒ a° = 1
Polynomials
⇒ (x+y)²=x²+2xy+y²
⇒ (x-y)²=x²-2xy+y²
⇒ (x+y)(x-y)=x²-y²
⇒ (x+a)(x+b)=x²+(a+b)x+ab
⇒ (x+a)(x-b)=x²+(a-b)x-ab
⇒ (x-a)(x+b)=x²+(-a+b)x-ab
⇒ (x-a)(x-b)=x²+(-a-b)x+ab
⇒ (x+y+z)²=x²+y²+z²+2xy+2yz+2zx
⇒ (-x+y+z)²=x²+y²+z²-2xy+2yz-2zx
⇒ (x-y+z)²=x²+y²+z²-2xy-2yz+2zx
⇒ (x+y-z)²=x²+y²+z²+2xy-2yz-2zx
⇒ (x+y)³=x³+y³+3x²y+3xy²
⇒ (x-y)³=x³-y³-3x²y+3xy²
⇒ x³+y³=(x+y)(x²-xy+y²)
⇒ x³-y³=(x-y)(x²+xy+y²)
⇒ x³+y³+z³=3xyz
⇒ x³+y³+z³-3xyz=(x+y+z)(x²+y²+z²-xy-yz-zx)
⇒ Area of Rectangle = Length×Breadth
⇒ Volume of Cuboid = Length×Breadth×Height
Linear Equations in Two Variables
⇒ General form of linear equation in two variables:- ax+by+c=0
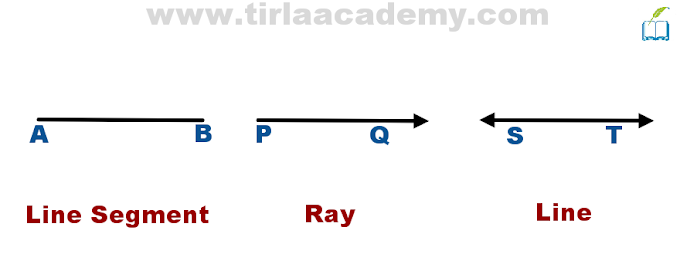
Lines and Angles
⇒ Zero Angle is 0°.
⇒ The right Angle is 90°.
⇒ Acute Angles are between 0° to 90°.
⇒ Obtuse Angles are between 90° to 180°.
⇒ Straight Angle is 180°.
⇒ Reflex angles are between 180° to 360°.
⇒ Complete Angle is 360°.
⇒ Sum of two complementary angles = 90°.
⇒ Sum of two supplementary angles = 180°.
⇒ When the sum of adjacent angles is 180° they are known as Linear pairs.
⇒ Vertically opposite angles are equal.
⇒ Straight line make 180° angle.
⇒ Exterior angle of triangle = Sum of its opposite interior angles.
⇒ Alternate interior angles are equal.
⇒ Sum of all interior angles in triangle = 180°
Triangles
⇒ Angles opposite to equal sides of an isosceles triangle are equal.
⇒ The side opposite to equal angles of a triangle are equal.
⇒ Sum of all interior angles in triangle = 180°
⇒ Each angle of equilateral triangle = 60°
Quadrilateral
Theorem 8.1: A diagonal of a parallelogram divides it into congruent triangles.
Theorem 8.2: In a parallelogram, opposite sides are equal.
Theorem 8.3: If each pair of opposite sides of a quadrilateral is equal, then it is a parallelogram.
Theorem 8.4: In a parallelogram, opposite angles are equal.
Theorem 8.5: If in a quadrilateral, each pair of opposite angles is equal, then it is a parallelogram.
Theorem 8.6: The diagonals of a parallelogram bisect each other.
Theorem 8.7: If the diagonals of a quadrilateral bisect each other, then it is a parallelogram.
Theorem 8.8: The line segment joining the mid-points of two sides of a triangle is parallel to the third side.
Theorem 8.9: The line drawn through the mid-point of one side of a triangle, parallel to another side bisects the third side.
Circles
Theorem 9.1: Equal chords of a circle subtend equal angles at the center.
Theorem 9.2: If the angles subtended by the chords of a circle at the center are equal, then the chords are equal.
Theorem 9.3: The perpendicular from the centre of a circle to a chord bisects the chord.
Theorem 9.4: The line drawn through the centre of a circle to bisect a chord is perpendicular to the chord.
Theorem 9.5: Equal chords of a circle are equidistant from the centre.
Theorem 9.6: Chords equidistant from the centre of a circle are equal in length.
Theorem 9.7: The angle subtended by an arc at the center is double the angle subtended by it at any point on the remaining part of the circle.
Theorem 9.8: Angles in the same segment of a circle are equal.
Theorem 9.9: If a line segment joining two points subtends equal angles at two other points lying on the same side of the line containing the line segment, the four points lie on a circle.
Theorem 9.10: The sum of either pair of opposite angles of a cyclic quadrilateral is 180°.
Theorem 9.11: If the sum of a pair of opposite angles of a quadrilateral is 180°, the quadrilateral is cyclic.
⇒ Pythagoras theorem:- H² = P² + B²
⇒ Sum of all interior angles in triangle = 180°
Heron's Formulas
⇒ The perimeter of the triangle= Sum of all sides
⇒ The perimeter Equilateral triangle= 3×Side
⇒ Area of Right-angled triangle=1/2×Base×Height
⇒ Area of triangle by Heron's formula=√[s(s-a)(s-b)(s-c)]
where s=semi-perimeter, & a,b,c=sides of the triangle.
⇒ Semiperimeter s=(a+b+c)/2
Surface Area and Volume
⇒ Diameter = 2×Radius
⇒ Radius = Diameter/2
⇒ Slant Height of cone l=√(r²+h²)
⇒ Radius of cone r=√(l²-h²)
⇒ Height of Cone h=√(l²-r²)
⇒ (CSA) Curved Surface Area of cone = 𝞹rl
⇒ (TSA) Total Surface Area of cone = 𝞹r(l+r)
⇒ Radius of Cone = CSA of Cone/𝞹l
⇒ Area of Rectangle = Length×Breadth
⇒ Surface Area of Sphere = 4𝞹r²
⇒ (CSA) Curved Surface Area of Hemisphere = 2𝞹r²
⇒ (TSA) Total Surface Area of Hemisphere = 3𝞹r²
⇒ Radius of Sphere = √(Surface Area/4𝞹)
⇒ (CSA) Curved Surface Area of Cylinder = 2𝞹rh
⇒ Volume of Cone = 1/3𝞹r²h
⇒ 1 litre = 1000cm³
⇒ Radius of Cone = √(3×Volume/𝞹h)
⇒ The volume of Sphere = 4/3𝞹r³
⇒ Volume of Hemisphere = 2/3𝞹r³
⇒ 1000 litre = 1m³
Statistics
⇒ Class-mark = (Upper Limit + Lower Limit)/2