Heron's Formula
Heron's formula is used to find the area of any type of triangles or quadrilaterals.
If we know the length of all sides of triangle & quadrilateral & also known the length of a diagonal of the quadrilateral.
The formula used to find the area of triangle & quadrilateral
HERON's FORMULA = √{s(s-a)(s-b)(s-c)}
Where,
s = semi-perimeter of a triangle
a, b & c = length of the sides of a triangle.
1. How to find the area of a triangle by Heron's Formula?
For finding the area of a triangle by Heron's formula we need the length of all sides of a triangle. For better understanding, we take an example.
Let's discuss-
Example:-
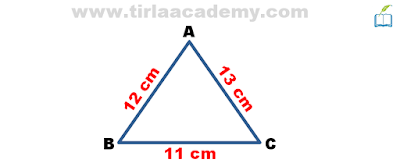
Find the area of a triangle if the length of its sides are 12 cm, 11 cm & 13 cm.
Solve:-
Given:-
Sides of triangle a=12cm, b=11cm & c=13cm.
Now, we will find the semi-perimeter of a triangle-
Semi-perimeter of a triangle s= (a+b+c)÷2
= (12+11+13)÷2
= 36÷2
s = 18cm
Put the value of a, b, c & s in the formula-
Area of triangle = √{s(s-a)(s-b)(s-c)}
= √{18(18-12)(18-11)(18-13)}
= √{18×6×7×5}
= √{108×35}
=√(3780)
=61.48 cm² approx.
2. How to find the area of a quadrilateral by Heron's Formula.
For finding the area of a quadrilateral by Heron's formula we need the length of all sides of a quadrilateral & length of one diagonal of a quadrilateral.
For better understanding, we take an example.
Let's discuss-
Example:-
Find the area of a quadrilateral if it's all sides are 13cm, 14cm, 12cm, 11cm & length of it's one diagonal is 16cm.
Solve:-
Given:-
Sides of quadrilateral are 13cm, 14cm, 12cm, 11cm & length of it's one diagonal is 16cm.
For finding the area of given quadrilateral ABCD we will find the area of triangles ABD & BCD & will add it.
Semi-perimeter of a triangle (ABD) s= (AB+BD+AD)÷2
= (13+16+11)÷2
= 40÷2
s = 20cm
Area of triangle (ABD) = √{s(s-a)(s-b)(s-c)}
= √{20(20-13)(20-16)(20-11)}
= √{20×7×4×9}
= √{140×36}
= √(5040)
= 70.99cm² approx.
Now, we will find the area of a triangle (BCD)
Semi-perimeter of a triangle (BCD) s= (BC+CD+BD)÷2
= (14+12+16)÷2
= 42÷2
s = 21cm
Area of triangle (BCD) = √{s(s-a)(s-b)(s-c)}
= √{21(21-14)(21-12)(21-16)}
= √{21×7×9×5}
= √{147×45}
= √(6615)
= 81.33cm² approx.
Total Area of Quadrilateral ABCD
= Area of ∆ABD + Area of ∆BCD
= 70.99cm² + 81.33cm²
= 152.32cm² approx.
So, the total area of ABCD is 152.32cm² approx.
For any query related to the article you may contact us & if it is helpful then please share.