COORDINATE GEOMETRY : How to find the distance between two points by Distance Formula?

UTPAL SHARMA

INTRODUCTION:-


In coordinate geometry, we study about the location or position of the point. We trace the position of a point with the help of coordinate of x & y.

We get coordinates with the help of x-axis(horizontal axis) & y-axis(vertical axis). In coordinate geometry, we may learn about the following-

  • Determine the distance between points ( By Distance Formula).
  • Area of a triangle.
  • Position of point between two points (Section Formula).


Terminology:-

Cartesian system

A plane on which we plot our graph & locate the point.
Cartesian System (COORDINATE GEOMETRY-How to find the distance between two points by Distance Formula)

Before go ahead read the picture carefully...

Horizontal axis(x-axis)

It is a line that is plot horizontally on the cartesian plane. It is also known as the x-axis.

Vertical axis(y-axis)

It is a line that is plot vertically on the cartesian plane. It is also known as the y-axis.

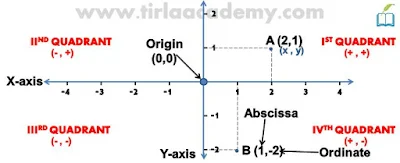
Origin

It is a common point (0,0) of the x-axis & y-axis.

Coordinate

Coordinate is a number or variable of the x-axis or y-axis. 

Abscissa

Coordinate of x is known as abscissa.

Ordinate

Coordinate of y is known as ordinate.

Quadrant

The cartesian plane is divide into four parts. Each part is known as a quadrant.

How to locate coordinates?

In the cartesian plane, we make reference to the x-axis & y-axis to locate the coordinates. Check the above picture for reference.
  • Let point A have coordinates (2,1) & remember, here 2 stands for abscissa (x coordinate) & 1 stand for ordinate (y coordinate).
  • We count 2 from the origin on the x-axis & count 1 from the origin on the y-axis.
  • Now take reference in the first quadrant because coordinates are lying in the first quadrant.
  • After reference, we get a point where the referencing line intersects each other.
  • As it is we may plot other points like B (1,-2), C (4,-4), D (-3,-2), etc.

How to find the distance between two points by Distance Formula?

Let us have two points on the cartesian plane whose coordinates are given.


Question:- 

Find the distance between two points whose coordinates are A(3,-4) & B(5,5).


Answer:-

First, we plot the above point for better understanding as shown below-
Distance A to B(COORDINATE GEOMETRY-How to find the distance between two points by Distance Formula)

Here we have the formula to find the distance between two points on the cartesian plane-

AB = √{(x₂-x₁)²+(y₂-y₁)²}

Where x₁=3, y₁=-4, x₂=5, y₂=5

Put the values of coordinate in the above formula for finding the distance AB-

AB = √{(5-3)²+(5-(-4))²}

AB = √{(2)²+(9)²}

AB = √{4+81}

AB = √85

The distance between points A & B is √85.

CONCLUSION:-

So now we know, how to get the distance between two points in the Cartesian plane. We may find the area of the triangle if it is plotted on cartesian plane. We may also divide a line in ratio or we may find the ratio of the divided line. We will discuss it in next blog.

Tags